Je me pose depuis quelques années la question de savoir pourquoi on nous dit toujours que les avalanches (de neige sèche sous forme de plaques) ne partent que sur des pentes supérieures à 30° ? À savoir s’il existe vraiment un angle de pente limite — minimal — pour qu’une avalanche de plaque sèche se déclenche ? Et si oui, pourquoi 30° ?
En furetant dans les entrailles de la littérature sur les avalanches, pour mon article précédent (« Quelques aspects de la physique des avalanches de plaque ») je suis tombé sur quelques publications qui donnent des éléments de réponse, que je vous livre ici.
La pente est un ingrédient essentiel dans le déclenchement d’une avalanche, elle sert de moteur : la pesanteur est en effet là pour tirer la neige, en rupture avec elle-même et avec son substrat, vers le bas.
Quelques observations
Dans son étude expérimentale des écoulements de neige sèche, Rognon (2006) a montré — entre bien d’autres choses — que sous une pente de 33°, la neige ne glisse plus.
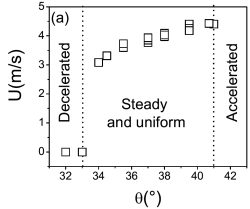
- Vitesse d’un flot de neige sèche en fonction de la pente.
- Vitesse moyenne d’un flot de neige sèche (grain fins) pour une épaisseur de 10 cm. Pour un angle inférieur à 33°, le flot s’arrête. Tiré de Rognon et al. (2008).
Cette partie de son étude est néanmoins à prendre avec des pincettes, malgré son grand intérêt elle pêche peut-être un peu par manque d’exhaustivité, et mériterait d’être complétée !
D’une part, la neige peut ne pas glisser sur des pentes plus raides, comme en témoigne l’image ci-dessous, où des résidus de plaque restent comme en suspens dans des pentes à 40° :

- Gros plan sur la zone de départ
- Plaque à vent déclenchée accidentellement sous les Pointes de la Porte d’Église. Au niveau de la zone de départ (environ 43°), on constate que certains blocs de neige (taille décimétrique) n’ont pas glissé.
D’autre part, on trouve un peu partout dans la littérature une distribution des pentes d’avalanches de plaques qui va jusqu’à des pentes de 25° : environ 1 % des avalanches de plaques partiraient sur des pentes de moins de 30° (voir figures ci-dessous).
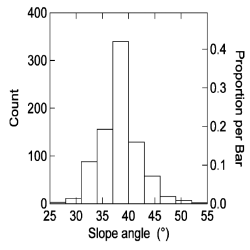
- Distribution des pentes d’avalanches
- Distribution des pentes d’avalanches déclenchées humainement à partir d’une base de 809 données provenant des montagnes Suisses et Canadiennes. Tiré de Schweizer et Jamieson (2001).
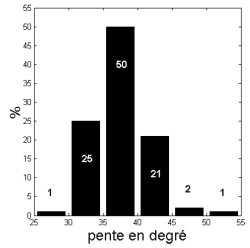
- Autre distribution des pentes d’avalanches
- Fraction des avalanches de plaque en fonction de l’angle de la pente de départ. Aucune information sur la source des données. Tiré de Faillettaz (2003).
McCammon a utilisé une base de données de 496 avalanches dans les montagnes des États-Unis entre 1972 et 2006 pour étudier différents aspects en fonction de l’angle de la pente de départ.
On constate qu’une fraction des avalanches de plaques, friables ou dures, part sur des pentes entre 25° et 30°. Malheureusement, nous n’avons pas d’autre information sur ces avalanches, ni sur la fraction en question.
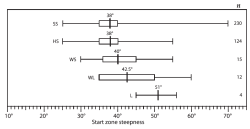
- Pente de départ en fonction du type d’avalanche
- Distribution des angles de départ d’avalanche en fonction du type d’avalanche (SS = plaque friable, HS = plaque dure, WS = plaque humide, WL = départ ponctuel humide, L = départ ponctuel sec), à partir d’une base de données de 496 avalanches entre 1972 et 2006 aux États-Unis. Tiré de McCammon 2009.
Ces avalanches qui partent sur des pentes à moins de 30° concernent pour l’essentiel des couches fragiles constituées de gobelets ou de givre de surface. Mais là encore, il manque des informations sur ces avalanches.
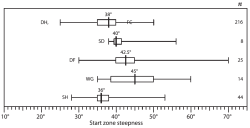
- Pente de départ en fonction de la nature de la couche fragile
- Distribution des angles de départ d’avalanche en fonction de la nature de la couche fragile (DH, FC = gobelet — givre de profondeur, SD = neige fraîche, DF = particules reconnaissables, WG = grains humides, SH = givre de surface), à partir d’une base de données de 496 avalanches entre 1972 et 2006 aux États-Unis. Tiré de McCammon 2009.
Si la distribution de ces 496 avalanches en fonction de l’angle est similaire à celle des distributions ci-dessus, on peut estimer à environ 1 % la fraction qui se déclenche sous 30°, soit 5 avalanches au total... Mais compte tenu de la petitesse de ce nombre, cela mériterait un examen minutieux (quelle est l’incertitude sur la mesure ou l’estimation de l’angle ? Celui-ci est-il bien mesuré au niveau de la zone de départ ? ... ?).
Dans tous les cas, il serait intéressant d’avoir plus d’information sur ces événements à moins de 30° : sont-ils « réels » ou bien résultat d’une incertitude de mesure ?
Théorie : l’approche tribologique
La tribologie est la science qui s’occupe des matériaux en contact, donc en particulier des frottements. J’en avais déjà un peu parlé à l’occasion de mon article sur l’escalade. Je vais me limiter ici au cas des frottements solides de type coulombiens.
Considérons une plaque de neige, sur une pente d’angle $\theta$ avec l’horizontale, de poids $\overrightarrow{P}=m\overrightarrow{g}$ où $m$ est la masse de la plaque et $\overrightarrow{g}$ l’accélération de la pesanteur. Elle est également soumise à une force de réaction, $\overrightarrow{N}$, perpendiculaire au substrat, et une force de frottement $\overrightarrow{T}$, parallèle à la pente et dirigée vers le haut.

- Équilibre de la plaque : forces en jeu
- Plaque en équilibre sur une faible pente : illustration des forces en jeu (poids P, réaction du substrat N, frottements T).
Dans le cas où la plaque est en équilibre, on a : $\overrightarrow{P} + \overrightarrow{N} + \overrightarrow{T} = \overrightarrow{0}$, soit, en projetant sur les deux axes, parallèle à la pente et perpendiculaire à la pente :
$N = P \cos \theta$ et $T = P \sin \theta$
On définit le coefficient de frottement statique comme $\mu_0 = \frac{T}{N}$, donc $\mu_0 = \tan \theta$.
Si la plaque glisse sur son substrat, avec une accélération $\overrightarrow{a}$, on a : $\overrightarrow{P} + \overrightarrow{N} + \overrightarrow{T} = m\overrightarrow{a}$ soit : $N = P \cos \theta$ et $-T + P \sin \theta = ma$

- Glissement de la plaque : forces en jeu
- Plaque en train de glisser sur son substrat : illustration des forces en jeu, avec l’accélération a résultante.
Le coefficient de frottement dynamique est donné par : $\mu = \frac{T}{N}$, soit : $-\mu P \cos \theta + P \sin \theta = ma$
Soit :
$\mu = \tan \theta - \frac{a}{g \cos \theta}$
Au passage, on constate que comme $a>0$ et $\cos \theta >0$, $\mu < \mu_0$ : le coefficient de frottement statique est plus important que le coefficient de frottement dynamique.
Van Herwijnen et Heierli en 2009 ont publié une étude expérimentale visant à mesurer le coefficient de frottement dynamique de différentes plaques de neige sur les débris des couches fragiles effondrées sous-jacentes. En filmant à grande vitesse le déplacement de plaques de neige soigneusement circonscrites ils ont pu déterminer leurs accélérations, et donc, en utilisant la relation ci-dessus, le coefficient de frottement dynamique $\mu$ correspondant.

- Illustration de la mesure du coefficient de frottement
- Première (a) et dernière (b) image d’une séquence de glissement filmée. Les points matérialisés permettent de reconstruire les variables cinématiques (position, vitesse, accélération) sur le film. Tiré de Herwijnen et Heierli (2009).
Les valeurs de $\mu$ obtenues en fonction de la pente mesurée sont représentées sur cette figure :
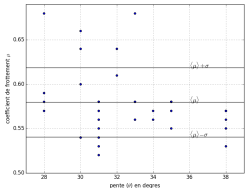
- Coefficient de frottement dynamique mesuré en fonction de l’angle de la pente
- Les points représentent les données de van Herwijnen et Heierli (2009). On représente aussi le coefficient de frottement moyen et son écart-type.
Ils obtiennent des valeurs de $\mu$ variant entre 0.52 et 0.68, relativement indépendante de l’angle de la pente (le coefficient de corrélation vaut -0.3), avec une valeur moyenne $\langle \mu \rangle$ = 0.58 et un écart-type de $\sigma_{\mu}$=0.04. Ce qui correspond à un angle limite de frottement de 30.1±1.7°.
Il faut noter cependant que cette valeur constitue une pente minimale pour la transition entre les « woufs » et l’avalanche (pas de glissement et glissement), car d’autres paramètres entrent en ligne de compte, la rugosité du sol, les frottements latéraux, etc, qui tendent à augmenter la valeur de cet angle.
On obtient néanmoins une explication simple de la fameuse valeur de « 30° » comme angle limite de déclenchement des avalanches.
Théorie : l’approche granulaire
Il y a quelques années (2009), Alain Duclos et ses collègues montrent que l’un des principaux constituants des couches fragiles, les gobelets (ou givre de profondeur) ont une propriété étrange : au repos, ils ont tendance à « coaguler » c’est-à-dire à se solidariser pour former un matériaux cohésif ; si on fournit de l’énergie à ce matériau (choc, pression...) il perd spontanément sa cohésion, et devient « liquide » comme le riz...
Louchet et al. (2013) modélisent ce matériau granulaire avec cette transition de phase entre liquide et agrégat solide. Ils trouvent qu’il existe une contrainte de cisaillement critique en-dessous de laquelle le matériau évolue toujours vers la forme solide, et au-dessus de laquelle le matériau évolue vers une phase globalement liquide mais contenant encore une fraction d’agrégats solides.
Dans le cas de la neige et des avalanches, la contrainte de cisaillement $\tau$ est la pesanteur, à savoir la composante parallèle à la plaque de neige (donc à la pente) du poids (par unité de surface) de la plaque ($\tau = \rho g h \sin \theta$ où $\rho$ est la masse volumique de la neige constituant la plaque, $g$ est l’accélération de la pesanteur, $h$ est l’épaisseur de la plaque et $\theta$ est l’angle de la pente).
À l’équilibre sous l’effet du poids de la plaque, les gobelets constituant la couche fragile restent sous un état solide. Rien ne bouge. Si la contrainte de cisaillement potentielle (pente et poids de la plaque) est suffisante, la moindre perturbation locale du « solide » gobelets va s’amplifier pour « fluidifier » le matériau et la plaque va ainsi pouvoir glisser. Au contraire, si la pente et le poids de la plaque sont insuffisants, la perturbation du matériau gobelets va s’estomper pour resolidifier le tout : rien ne bouge.
Un rapide calcul quantitatif pour des valeur ad-hoc des différents paramètres montre que la fluidification a lieu pour un intervalle de valeurs de la pente entre 28° et 62° : en deçà, le cisaillement est trop faible, au-delà, la haute de neige tend vers zéro. Même si on trouve un angle limite proche des fameux 30°, une étude quantitative plus exhaustive mériterait d’être faite autour de ce modèle.
L’énergie nécessaire pour passer de la phase solide à la phase liquide est mesurée par les auteurs à l’aide d’une expérience toute simple. Ils obtiennent 200 à 300 J/m3.
L’énergie cinétique d’un skieur de 80 kg qui descend à 30 km/h = 8 m/s est de 2,8 kJ. On suppose que toute cette énergie est transféré au manteau neigeux lors d’une chute où d’un virage.
Or le volume d’une couche fragile de 5 mm d’épaisseur et 104 m2 est de 50 m3. Il faut donc une énergie de 50 × 250 = 12,5 kJ pour « actionner » la transition de phase solide —> liquide : le skieur n’est pas suffisamment « énergétique » pour déclencher l’avalanche. Mais si on considère une plaque de 50 × 50 m2, on obtient le même ordre de grandeur que l’énergie du skieur...
Louchet el al. (2013) concluent que l’approche de van Herwijnen (2009) avec des frottements solides est criticable compte tenu de l’observation de la grosse discontinuité de viscosité des gobelets entre la phase « fluide » ($\sim$ 10 Pa⋅s) et la phase « solide » ($\sim$ 105 Pa⋅s).
Le modèle de Louchet el al. (2013) semble avoir en plus le mérite d’expliquer le fait que certaines plaques commencent à glisser avant de s’arrêter même sur des pentes « raides » (observés par van Herwijnen (2009)) et sur la photo ci-dessus, où l’on voit des morceaux de plaques à l’arrêt sur des pentes avoisinant les 40° ! Le modèle des frottements solides de Coulomb ne permet pas d’expliquer ça, car le coefficient de frottement dynamique (et donc l’angle limite de frottement) ne dépend pas du poids de la plaque. Or le modèle de Louchet dépend de la contrainte de cisaillement, donc du poids de la plaque : une assemblée de gobelets mise sous forme fluide par une certaine contrainte ponctuelle (poids total de la plaque et pente) peut retourner sous forme solide si la contrainte devient insuffisante (fragmentation de la plaque, absence d’effet « chasse-neige »).
Dans les deux modèles l’angle limite pour qu’une avalanche se produise est autour de 30°, mais il faudrait le préciser dans le modèle de Louchet en explorant plus finement l’espace des paramètres. Il serait également particulièrement intéressant de confronter ce modèle aux paramètres cinématiques des avalanches mesurés, comme dans van Herwijnen (2009).
Conclusion
Je vais terminer là (pour le moment) cette série d’études bibliographiques sur les avalanches de plaques. J’ai découvert un champ de recherche riche et foisonnant, qui me donnerait presque envie de me reconvertir !
Car à la lumière de ce que j’ai pu lire, notamment ici sur les pentes, il reste, à mon avis, nombre d’études à mener pour comprendre l’effet de la pente, vérifier expérimentalement à l’aide de bases de données précises et conséquentes si l’angle de 30° constitue bel et bien une limite ou pas, etc.





