La fréquence avec laquelle on trouve des galaxies de luminosités intrinsèques différentes est décrite par leur fonction de luminosité $\Phi(M)$. La quantité $\Phi(M) dM$ est ainsi proportionnelle au nombre de galaxies qui ont une magnitude absolue dans l’intervalle $[M,M+dM]$.
En pratique la fonction de luminosité est normalisée à l’unité de volume :
$\Phi(M) dM = \frac{dN}{dV}$,
$dN$ étant le nombre de galaxie de magnitude absolue $M \in [M,M+dM]$.
La fonction de luminosité des galaxies est un ingrédient observationnel important, tant du point de vue cosmologique que pour comprendre la formation et l’évolution des galaxies. Elle contient des informations primordiales sur le spectre de puissance des fluctuations de densité primordiales, sur les processus physiques qui convertissent la masse en lumière (comme par exemple l’effondrement gravitationnel, le refroidissement et la formation des étoiles), sur les mécanismes qui détruisent, génèrent ou modifient la morphologie des galaxies (interactions de marée, fusion...). Ainsi cet outil est nécessaire pour interpréter l’énorme population de galaxies bleues faiblement brillantes découverte aux décalages spectraux intermédiaires [1] ($z \sim 0.5$), pour estimer les densités de luminosité et de baryons dans l’Univers et pour tester les modèles de formation et d’évolution des galaxies.
Les galaxies du champ
La détermination de la fonction de luminosité des galaxies de champ est une manœuvre délicate qui doit tenir compte des corrections K, du biais de Malmquist (les relevés limités en magnitude vont manquer les galaxies de plus faible luminosité), des vitesses particulières (surtout pour les galaxies proches) ainsi que de la répartition spatiale non-homogène des galaxies (mais plutôt sur des murs, autour de grand vides).
La fonction de Schechter
Une fois tous ces paramètres pris en compte, la fonction de luminosité prend une forme relativement simple qui est assez bien représentée par une fonction de Schechter (Schechter 1976) :
$\Phi(L) = \frac{\Phi^*}{L^*} \left(\frac{L}{L^*} \right)^{\alpha} \exp \left(-\frac{L}{L^*} \right)$
$L$ étant la luminosité des galaxies ; $\Phi^*$, $L^*$ et $\alpha$ étant choisis pour décrire les observations. Cette relation s’exprime en magnitude absolue selon :
$\Phi(M) = (0.4 \ln 10) \Phi^* 10^{0.4 (\alpha + 1) (M^*-M)} \exp \left(-10^{0.4(M^*-M)} \right)$
o\`u $M^*$ est la magnitude absolue correspondant \`a $L^*$.
$\alpha$ correspond ainsi à la pente de la fonction de luminosité vers les luminosités les plus faibles, $L^*$ ou $M^*$ donne la luminosité caractéristique au-delà de laquelle le nombre de galaxies diminue drastiquement, et $\Phi^*$ normalise la densité de galaxies.
Avec ce paramétrage, la densité moyenne de luminosité s’exprime selon :
$\rho_L = \int_0^{+\infty} L \Phi(L) dL = \Phi^* L^* \Gamma(\alpha+2)$
o\`u $\Gamma$ est la fonction gamma [2]. Elle dépend du modèle cosmologique choisi \`a travers $\Phi^*$ et $L^*$, respectivement proportionnels \`a l’inverse du volume comobile et au carré de la distance de luminosité.
En supposant que la fonction de luminosité est indépendante de la localisation et que les galaxies sont distribuées de façon homogène, le nombre total de galaxies jusqu’à la magnitude apparente limite $m$ est, dans le cas non-relativiste, donné par :
$\mathcal{N}_{ o\`u $d^*(m)$ est la distance correspondant à la profondeur limite
du relevé pour une galaxie de luminosité $L^*$ ; ainsi $d^*(m)
\propto {L^*}^{1/2}$. La luminosité des galaxies dans le domaine visible s’étend sur une
gamme extrêmement grande, entre les galaxies elliptiques géantes
telle M87 au centre de l’amas de la Vierge, avec $L_B \sim 5\cdot
10^{10}\ \text{L}_{\odot}$ ($M_B \sim -22$) et les galaxies
elliptiques naines, dont la luminosité ($M_B \sim -7.5$) est
comparable à celle d’une étoile massive sur la séquence
principale. Le relevé LCRS a publié une mesure de la
fonction de luminosité des galaxies de champ
(Lin et al., 1996). Les paramètres de la fonction de Schechter
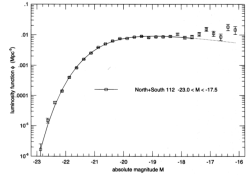
obtenus, dans la bande [3] $R_c$, sont les suivants : $M^* = -20.29 \pm 0.02 + 5\ \log h $ $\alpha = -0.70 \pm 0.05 $ $\phi^* = 0.019 \pm 0.001\ h^3\ \text{Mpc}^{-3} $ pour $-23 \le M- 5 \log h \le -17.5$. Sur ce même intervalle de
magnitude absolue, la densité moyenne de galaxies est
0.029$\pm0.002\ h^3\ \text{Mpc}^{-3}$ pour un volume jusqu’à
$z = 0.2$. La densité moyenne de luminosité galactique est $\rho_L
= 1.4\pm 0.1 \cdot 10^8\ h\ \text{L}_{\odot}\cdot \text{Mpc}^{-3}$ dans la
bande $R_c$. La
fonction de luminosité est représentée sur la figure suivante : Notons que le LCRS trouve des différences significatives entre la
population de galaxies avec raies d’émission et sans raies
d’émission. Les galaxies à raies d’émission dominant la partie
à faible luminosité de la fonction de luminosité. Il existe de nombreux autres relevés qui ont publié une fonction
de luminosité des galaxies. Notons le ESO Slice Project
galaxy redshift survey (Zucca et al., 1997), avec une fonction de
luminosité dans la bande $B_j$, ajustée par une fonction de
Schechter et une loi de puissance pour ajuster l’excès de population
dans la partie faibles luminosités. Le 2dF Galaxy Redshift Survey (Madgwick et al., 2002) donne
une fonction de luminosité dans la bande $B_j$ pour différentes
classes de galaxies, basées sur l’importance moyenne des raies
d’émission et d’absorption, un indicateur du taux de
formation d’étoiles. Ils observent ainsi un redressement de la
pente $\alpha$ de la fonction de luminosité du côté des faibles
luminosités depuis les galaxies formant des étoiles passivement
($\alpha = -0.55$) jusqu’aux galaxies formant des étoiles activement
($\alpha = -1.36$). Observations
La fonction de luminosité du LCRS
Autres relevés...