Accueil > Science > Thermodynamique

Température d’ébullition de l’eau en altitude

samedi 21 mai 2011 par Guillaume Blanc

Sommaire

Nos dernières aventures nous ayant fait découvrir le monde de la haute altitude, je vous livre ici quelques réflexions crayonnées un après-midi assis sur une pierre au soleil, sur la température d’ébullition de l’eau en fonction de l’altitude.

Équilibre hydrostatique d’une couche d’air

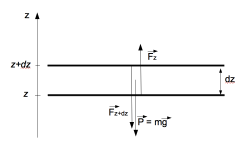
Il s’agit dans un premier temps de déterminer l’évolution de la pression atmosphérique en fonction de l’altitude. Pour ce faire, on regarde une petite couche d’air, à l’altitude , d’épaisseur , et de surface , sur laquelle on fait un bilan des forces appliquées. Ces forces sont de deux types, les forces pressantes, et la force de pesanteur. Il y a donc la force de pression de tout l’air au-dessus de la petite couche $\overrightarrow{F_P}(z+dz)$ , dirigée vers le bas, la force de pression de tout l’air en-dessous de la couche, $\overrightarrow{F_P}(z)$ , dirigée vers le haut. Les forces de pression latérales s’annulent deux à deux. La force de pesanteur est $m\overrightarrow{g}$ , étant la masse de la couche d’air et $\overrightarrow{g}$ l’accélération de la pesanteur.

**Bilan des forces sur une petite couche d’air**

Comme notre petite couche d’air est à l’équilibre, le Principe Fondamental de la Dynamique donne :

$\overrightarrow{F_P}(z+dz) + \overrightarrow{F_P}(z) + m\overrightarrow{g} = \overrightarrow{0}$ soit, en projetant sur un axe vertical dirigé vers le haut :

, et avec $F_P(z) = S \cdot P(z)$ où est la pression régnant à l’altitude , on a :

Soit $P(z+dz) - P(z) = -\frac{mg}{S}$ ; or $m = \rho \cdot S \cdot dz$ , $\rho$ étant la masse volumique de l’air, donc on obtient : $\frac{P(z+dz) - P(z)}{dz} = - \rho \cdot g$ soit : $\frac{dP}{dz} = -\rho \cdot g$ .

L’air troposphérique pouvant être considéré comme un gaz parfait avec une bonne approximation (pression faible, peu de collisions entre les molécules), on a : $PV = nRT = \frac{mRT}{M}$ , où est la masse de gaz considéré, $M_{\mathrm{air}}$ sa masse molaire. Soit : $\rho = \frac{PM_{\mathrm{air}}}{RT}$ .

Il s’agit donc désormais d’intégrer l’équation : $\frac{dP}{P} = - \frac{M_{\mathrm{air}}g}{RT}dz$ ; mais pour ce faire, il faut déterminer l’évolution des paramètres et en fonction de l’altitude . On peut raisonnablement faire l’approximation que l’accélération de la pesanteur ne varie pas sur les altitudes considérées, qui sont celles de la troposphère, typiquement. Or l’épaisseur de la troposphère varie entre 6 et 20 km selon la latitude.

En revanche la température varie dans cette couche atmosphérique. Elle diminue typiquement linéairement, depuis 15 °C, en moyenne, au niveau de la mer, avec un gradient de -6.5 °C/km.

Variation de la température avec l’altitude

Une bonne modélisation de cette partie de l’atmosphère est de considérer que le petit volume d’air ci-dessus n’échange pas d’énergie thermique avec son environnement (il échange seulement du travail), ce qui revient à dire que les transformations qu’il subit sont adiabatiques.

En considérant une transformation adiabatique et réversible pour notre petit volume d’air qui se comporte comme un gaz parfait, on a la loi de Laplace : $P\cdot T^{\frac{\gamma}{1-\gamma}} =$ cte, que l’on dérive pour obtenir : $\frac{dP}{P} = \frac{\gamma}{\gamma - 1} \frac{dT}{T}$

En remplaçant dans la relation obtenue plus haut, on obtient : $dT = \frac{1-\gamma}{\gamma} \frac{M_{\mathrm{air}}g}{R}dz$ , soit : $T(z) = T_0 + \frac{1-\gamma}{\gamma} \frac{M_{\mathrm{air}}g}{R} \cdot z$ . La température se comporte donc de manière linéaire dans la troposphère, sous l’hypothèse d’adiabaticité, qui correspond à l’air stable. Le coefficient $a_T = \frac{1-\gamma}{\gamma} \frac{M_{\mathrm{air}}g}{R}$ est le gradient thermique adiabatique pour l’air sec.

Le gradient thermique

L’air étant composé principalement d’un mélange de deux gaz diatomiques, le dioxygène et le diazote, le coefficient $\gamma$ correspondant vaut environ 1.4 (et ce avec une bonne approximation) ; la masse molaire de l’air vaut $M = 29\ \mathrm{g}\cdot \mathrm{mol}^{-1}$ , l’accélération de la pesanteur vaut : $g = 9.8\ \mathrm{m}\cdot \mathrm{s}^{-2}$ et la constante des gaz parfait vaut : $R = 8.31\ \mathrm{J}\cdot \mathrm{K}^{-1}\cdot \mathrm{mol}^{-1}$ . Ce qui donne un gradient adiabatique de = -9.97 K/km.

**L’atmosphère**

Profil atmosphérique moyen en température et pression, en fonction de l’altitude.

En réalité, le gradient thermique moyen dans la troposphère vaut -6.5 K/km, la différence venant du fait que l’atmosphère réelle contient une certaine quantité de vapeur d’eau. La température baissant avec l’altitude, cette vapeur d’eau va se condenser. Or la chaleur latente de liquéfaction étant négative, cette transformation est exothermique et va réchauffer l’atmosphère. Et ainsi diminuer en valeur absolue le gradient thermique, par rapport à une atmosphère sèche comme calculé ci-dessus.

L’évolution de la pression avec l’altitude

En reportant l’expression de la température, $T(z) = T_0 + a_T \cdot z$ , dans l’expression de l’équilibre hydrostatique ci-dessus, cela donne : $\frac{dP}{P} = -\frac{M_{\mathrm{air}}g}{R(T_0 + a_T\cdot z)}dz$ . Ce qui donne, en intégrant entre le niveau de la mer ( $z = 0, P = P_0,\ T = T_0$ ) et l’altitude : $\ln \frac{P}{P_0} = - \frac{M_{\mathrm{air}}g}{R a_T}\ln \left(1 + \frac{a_T z}{T_0} \right)$ , soit :

$P(z) = P_0 \left(1 + \frac{a_T z}{T_0} \right)^{-\frac{M_{\mathrm{air}}g}{R a_T}}$ ;

Dans le cas adiabatique, $a_T = \frac{1-\gamma}{\gamma} \frac{M_{\mathrm{air}}g}{R}$ soit : $P(z) = P_0 \left(1 - \frac{\gamma-1}{\gamma} \frac{z}{z_0}\right)^{\frac{\gamma}{\gamma - 1}}$ où $z_0 = \frac{RT_0}{M_{\mathrm{air}}g} = 8\ \mathrm{km}$ est l’échelle caractéristique de hauteur de la troposphère.

Hypothèse isotherme

Une simplification habituelle consiste à supposer que la température ne varie pas avec l’altitude (atmosphère isotherme). Dans ce cas, on peut intégrer directement l’équation : $\frac{dP}{P} = - \frac{M_{\mathrm{air}}g}{RT_0}dz$ , ce qui donne :

$P(z) = P_0 \exp \left( -\frac{M_{\mathrm{air}}g}{RT_0} z \right)$

La formule de Clapeyron

La relation de Clapeyron donne l’évolution de la pression d’équilibre en fonction de la température d’équilibre d’un corps au cours d’un changement d’état.

Pour le passage entre l’eau liquide et la vapeur d’eau (vaporisation) qui nous intéresse ici, elle est donnée par :

$l_v = T(v_g - v_l) \frac{dP_s}{dT}$ , où est la chaleur latente massique de vaporisation de l’eau, est le volume massique de la vapeur d’eau, est le volume massique de l’eau liquide, et est la pression de vapeur saturante.

Démonstration

Une démonstration possible de la formule de Clapeyron est la suivante.

L’énergie interne d’un système est donnée par : $U = TS - PV + \mu N$ , où est l’entropie, $\mu$ le potentiel chimique et le nombre totale de particules.

Le Premier Principe donne la variation élémentaire d’énergie interne, comme : $dU = TdS -PdV+\mu dN$ . Or en différentiant la première relation, cela donne : $dU = TdS + SdT -PdV - VdP + \mu dN + N d\mu$ , que l’on soustrait à celle donnée par le Premier Principe : $0 = SdT - V dP + N d\mu$ . Cela donne la relation de Gibbs-Duhem : $d\mu = v_n dP - s_n dT$ , où est le volume molaire et est l’entropie molaire.

Lors d’un changement de phase, il y a équilibre entre les deux phases, gazeuse et liquide, par exemple, d’où égalité des potentiels chimiques : $\mu_g = \mu_v$ , soit $d\mu_g = d\mu_v$ .

Ce qui donne, d’après la relation de Gibbs-Duhem : . Soit, finalement : $s_n^l - s_n^g = (v_n^l - v_n^g) \frac{dP_s}{dT}$ . Or, par définition de la chaleur latente, on a : $l_n^v = T \Delta_n = T (s_n^l - s_n^g)$ , où est la chaleur latente molaire de vaporisation. Ainsi : $l_n^v = T (v_n^l - v_n^g) \frac{dP_s}{dT}$ .

Expression que l’on peut diviser de part et d’autre par le rapport masse molaire sur le nombre d’Avogadro pour obtenir une expression « massique » :

$l_v = T (v_g - v_l) \frac{dP_s}{dT}$ .

Cette relation, dans le cas où le volume massique de gaz est très grand devant celui du liquide, comme c’est le cas pour l’eau, peut s’écrire : $\frac{dP_s}{dT} \simeq \frac{l_v}{T\cdot v_g}$ , avec $v_g = V/m = nRT/(mP) = RT/(M_{\mathrm{eau}} P)$ , soit :

$\frac{dP_s}{dT} \simeq \frac{l_v M_{\mathrm{eau}}}{RT^2} P$ , ce qui donne, en intégrant — en supposant que la chaleur latente est constante, ce qui est discutable [1] — la relation entre la pression de vapeur saturante, qui est aussi la pression de l’air ambiant, et la température d’ébullition :

$\ln \frac{P(T)}{P_0} = \frac{l_v M_{\mathrm{eau}}}{R} \left(\frac{1}{T_e} - \frac{1}{T} \right)$ , où est la température d’ébullition au niveau de la mer ().

Température d’ébullition en fonction de l’altitude

En combinant les relations $P(z) = P_0 \left(1 + \frac{a_T z}{T_0} \right)^{\frac{Mg}{R a_T}}$ et $\ln \frac{P(T)}{P_0} = \frac{l_v M_{\mathrm{eau}}}{R} \left(\frac{1}{T_e} - \frac{1}{T} \right)$ , on obtient :

$T(z) = \left(\frac{1}{T_e} + \frac{g M_{\mathrm{air}}}{l_v a_T M_{\mathrm{eau}}} \ln \left( 1+ \frac{a_T}{T_o} z \right) \right)^{-1}$

Si on considère une atmosphère isotherme, alors :

$T(z) = T_e \left(1 + \frac{M_\mathrm{air} g T_e}{l_v M_{\mathrm{eau}}T_0} z \right)^{-1}$ .

J’ai tracé ces différents modèles sur le graphe ci-dessous, avec les valeurs numériques suivantes : la température d’ébullition de l’eau au niveau de la mer $T_e = 100\ ^\circ\mathrm{C} = 373\ ^\circ\mathrm{K}$ , la température moyenne au niveau de la mer $T_0 = 15\ ^\circ\mathrm{C} = 288\ ^\circ\mathrm{K}$ , la masse molaire de l’eau $M_{\mathrm{eau}} = 18\ \mathrm{g}\cdot \mathrm{mol}^{-1}$ , la chaleur latente massique de vaporisation de l’eau $l_v = 2.27\ \mathrm{MJ}\cdot \mathrm{kg}^{-1}$ .

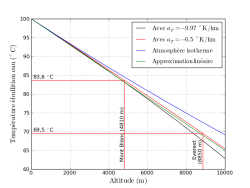
**Température d’ébullition de l’eau en fonction de l’altitude**

Pour les différents modèles présentés ici : adiabatique sec (avec un gradient thermique de -9.97 K/km), adiabatique humide (avec un gradient thermique de -6.5 K/km) et isotherme. En sus une très bonne approximation linéaire...

On constate que quel que soit le modèle décrit, les résultats sont très similaires, en tout dans une gamme d’altitudes « accessibles. »

De surcroît, une approximation linéaire s’avère très bonne : $T(z) = T_e - 0.0035 \times z$ .

Ainsi on peut retenir que la température d’ébullition décroit environ de 3.5 °C par kilomètre.

Quant à savoir si à l’altitude typiques des camps de base de l’Himalaya (5000 m), la température d’ébullition de 83 °C suffit pour tuer les potentiels agents pathogènes ? Ma foi, en tout cas, nous n’avons pas été malade !

[1] Entre 0.5 et 1 bar la chaleur latente de vaporisation de l’eau varie entre 2305.42 kJ/kg et 2257.92 kJ/kg soit une variation de 2 %, largement dans les limites du modèle proposé ici !