Le rayonnement de la neige
En rapatriant (octobre 2025) des articles de l’ancien vers le nouveau blog, je suis tombé sur cet article, écrit il y a plus de 10 ans. Je me demande pourquoi je ne l’ai jamais publié. Ainsi est fait.
L’alpiniste printanier, sillonnant la haute montagne, le sait pertinemment : une bonne nuit claire et au petit matin, la neige qui s’accroche encore à la montagne sera dure comme du béton, gage de sécurité sur une course de « neige. » Les crampons mordent facilement, le pas est assuré et ne s’enfonce pas. La neige ne bouge pas. La traversée d’un glacier n’en sera que plus sécuritaire, les ponts de neige au-dessus des crevasses sont solides ; les pentes et couloirs restent ainsi en place, la cohésion de la neige gelée lui permettant de lutter efficacement contre la gravité. Bref, tout est pour le mieux.
La neige est sous forme de névé : au cours du temps, la température généralement positive en journée a augmenté la quantité d’eau liquide dans le manteau neigeux, les grains de neige, amalgames de cristaux ayant déjà subit maintes transformations mécaniques et thermodynamiques, se retrouvent sous la forme de petits grains de glace, dits grains ronds. Au gré du gel et du dégel, ces grains ronds se maintiennent les uns aux autres soit par cohésion capillaire, si la neige contient suffisamment d’eau liquide (plus de 3-4 % en volume), soit par cohésion de regel quand les ponts d’eau entre les grains gèlent.
La cohésion capillaire n’est pas suffisamment importante pour supporter le poids de l’alpiniste, qui va donc s’enfoncer. Selon l’inclinaison de la pente et la teneur en eau liquide de la neige ainsi liée, celle-ci peut glisser en avalanche sur la pente. Ce sont les avalanches de neige humide qui ont lieu le plus souvent au printemps aux heures les plus chaudes de la journée (fonte maximale, teneur en eau liquide importante).
C’est donc une cohésion de regel que va rechercher l’alpiniste. Cette cohésion a lieu à partir du moment où les ponts capillaires, liquides, se solidifient. Ainsi la neige sèche, et va permettre ainsi de supporter le poids de l’alpiniste. Ce que celui-ci recherche dans ses inutiles ascensions.
Que les étoiles brillent toute la nuit, firmament éthéré, et malgré des nuits parfois « chaudes » en haute montagne (en été l’isotherme zéro degrés celsius peut passer la nuit bien au-delà de 4000 m), la neige regèle.
Comment cela se fait-il ? L’autre observation, pendante, est que si la nuit est nuageuse, ciel « bâché, » la neige reste molle, humide, avec pour seule cohésion, celle des ponts capillaires et donc potentiellement dangereuse.
Pour que la neige regèle, il faut que l’eau qu’elle contient dû à la fonte journalière, se transforme en glace, donc qu’elle se solidifie. La solidification de l’eau liquide est une transformation thermodynamique exothermique, c’est-à-dire qu’elle libère de la chaleur. C’est donc peu ou prou cette chaleur-là qu’il va falloir évacuer pour que la neige se solidifie.
Le transport de la chaleur — et donc son évacuation — peuvent se faire selon trois mécanismes distincts. Dans les milieux matériels, elle peut se faire par conduction, l’agitation thermique des atomes ou molécules dépendant de la températures, si celle-ci n’est pas uniforme, l’énergie cinétique des particules va pouvoir se propager de proche en proche, diffusant ainsi la chaleur.
Dans un fluide, la chaleur peut également se propager par convection. Une différence de température dans le sens de l’accélération de la pesanteur — chaud en bas, froid en haut —, comme la masse volumique d’un fluide dépend de sa température, la poussée d’Archimède va ainsi induire un mouvement de rotation du fluide, entre le bas et le haut, transportant la chaleur de la partie chaude (le bas) vers la partie froide (le haut). La convection dite naturelle (échange de chaleur sous l’effet d’une différence de température) n’est pas toujours très efficace. Elle peut néanmoins être forcée si le vent se lève...
Enfin la dernière façon de transporter de la chaleur est le rayonnement. Tous les corps émettent un rayonnement électromagnétique en fonction de leur température. Une classe de corps « idéaux, » les corps noirs, absorbent toute l’énergie électromagnétique qu’ils reçoivent. Ils la ré-émettent selon un spectre qui dépend uniquement de leur température. Ce spectre est large et couvre plusieurs gammes de longueurs d’onde, mais il présente un maximum autour duquel la majorité du rayonnement est émis.
Plus un corps est froid, plus le rayonnement émis est à grande longueur d’onde. Ainsi, le Soleil, d’une température de surface de 5800 K, émet principalement à 0,5 μm, c’est-à-dire juste au milieu de l’intervalle de la lumière visible sur lequel nos yeux sont sensibles ! Notre corps, bien plus froid, à 37°C = 310 K, émet principalement dans l’infrarouge dit thermique, à 9,35 μm. Notre œil est insensible à ces longueurs d’ondes, c’est pourquoi nous ne voyons pas la « chaleur » que nous dégageons. Nous voyons seulement la lumière visible du Soleil (ou de l’éclairage artificiel) qui se reflète sur nous.
Revenons à notre névé. Celui-ci peut se refroidir à travers l’air atmosphérique qui le surmonte. Cet air est un milieu matériel fluide (gazeux) et transparent. La chaleur issue du névé peut donc s’y propager selon les trois mécanismes présentés ci-dessus : conduction, convection, rayonnement. La conduction, dans l’air, est généralement beaucoup moins efficace que les deux autres processus, on peut la négliger allègrement.
Quant à la convection, elle existe, mais ce n’est pas le mécanisme prépondérant. En effet, celle-ci n’a pas de raison de dépendre de la couverture nuageuse, si elle était à l’origine de l’évacuation de la chaleur de solidification de la neige humide, cela fonctionnerait qu’il fasse beau ou pas[1]. Donc l’explication doit venir plutôt du dernier processus, le rayonnement. Nous allons voir qu’il dépend effectivement de la couche nuageuse.
La neige humide est typiquement à une température de 0 °C (mélange d’eau liquide et de glace). Elle rayonne donc essentiellement à 10,6 μm, dans l’infrarouge thermique. La puissance qu’elle émet par unité de surface est donnée par la loi de Stefan :
, où est la constante de Stefan.
Elle reçoit également la puissance radiative émise par le ciel . Ainsi la puissance nette émise par la neige est donnée par :
.
Ainsi, si , , donc la neige envoie du rayonnement vers le ciel... Elle perd de l’énergie. Et inversement si .
Donc tout va venir de la température du ciel. Si elle est inférieure à 0 °C, la température de la neige en fin de journée, la neige pourra se refroidir, si elle est supérieure à 0 °C, elle va se réchauffer, et donc être dans l’impossibilité de solidifier ses ponts aqueux pour assurer une solidité renforcée de l’édifice neigeux.
Shaw et al. (2005) montrent des images du ciel dans l’infrarouge thermique (autour de 10 μm) pour différentes couvertures nuageuses.
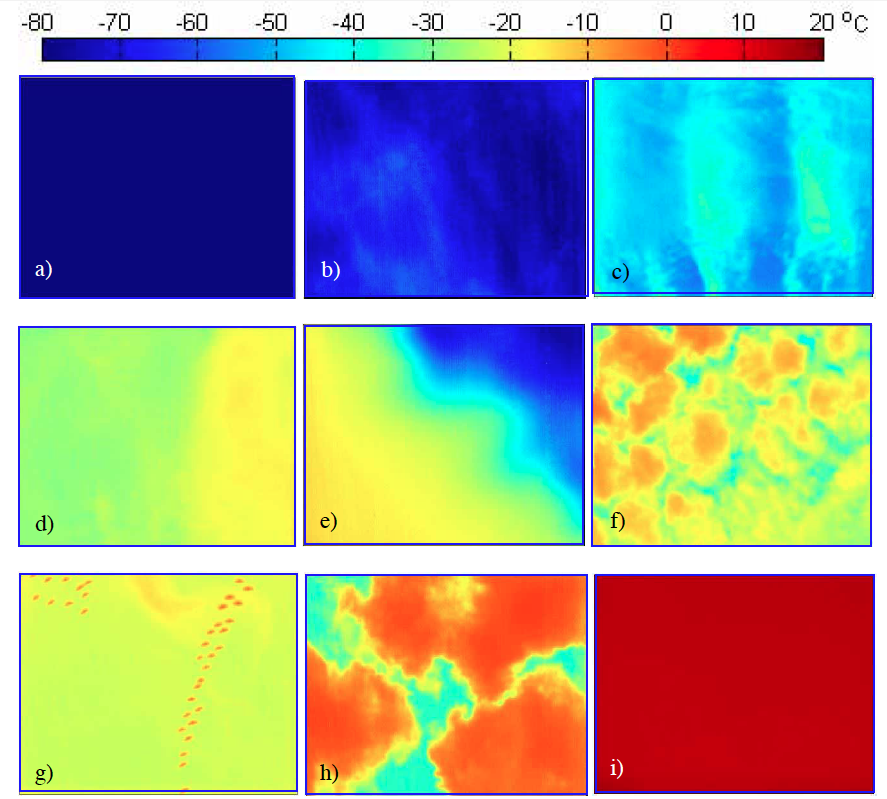
Température du ciel et des nuages. Images de différents ciels avec une caméra thermique. a) ciel froid, clair ; b) fins cirrus ; c) vagues d’altocumulus ; d) différents nuages altostratus ; e) bord d’une nappe de stratus ; f) altocumulus ; g) oiseaux volants sous des cirrus épais ; h) mélange de nuages de basse et moyenne altitude ; i) Stratus épais de basse altitude. Les images sont codées en couleur selon la température : bleu = -80 °C et rouge = +20 °C. Tiré de Shaw et al. (2005).
On peut comprendre les différentes températures liées aux différents types de nuages :
- ciel clair = -80 °C
- fins cirrus = -70 °C
- alto-cumulus = -30 °C à -50 °C
- alto-stratus = -20 °C à -30 °C
- stratus = -20 °C
- alto-cumulus = -10 °C
- cirrus épais = -20 °C
- stratus épais = +10 °C
En effet, chaque type de nuage est grosso modo rattaché à une certaine altitude, chaque altitude correspondant à peu près à une certaine température[2].

Les différents types de nuages dans l’atmosphère. Source : https://
Ainsi :
- les cirrus (Ci) se baladent vers 9 km, à °C
- les cirro-stratus (Cs) vers 8 km, à °C
- les cirro-cumulus (Cc) vers 6-7 km, à °C
- les alto-stratus (As) vers 4 km, vers -10 °C
- les strato-cumulus (Sc) vers 1-2 km, vers °C
- les cumulo-nimbus (Cb) entre 1 et 10 km,
- les cumulus (Cu) entre 1 et 3 km,
- les stratus au niveau du sol (15 °C)
Ces valeurs sont à titre d’illustration. Les altitudes d’un type de nuages peuvent fortement varier, les températures en fonction de l’altitude aussi, en fonction de la latitude, de la saison, de la météo, etc.
Toujours est-il que le ciel clair a à peu près une température de -80 °C.
À priori, la neige va perdre de l’énergie tant que la température du ciel est inférieure à 0 °C. Cette perte d’énergie, pour être « utile » à l’alpiniste, doit être suffisante pour solidifier le manteau neigeux.
Faisons un petit calcul, celui du temps mis pour solidifier le névé.
Considérons une surface de 1 m de neige, sur une épaisseur de 20 cm[3]. La masse volumique de la neige de névé est environ de 500 kg/m, ce qui nous fait 100 kg de neige. En fin d’après-midi ensoleillé, cette neige est typiquement très humide, supposons qu’elle contienne 4 % en masse d’eau liquide, soit 4 kg d’eau liquide.
L’énergie nécessaire pour geler ces = 4 kg d’eau (tout en les conservant à une température de 0 °C) est donnée par : , où est la chaleur latente de solidification de l’eau liquide (), soit 1332 kJ.
Maintenant, si on suppose que le ciel est clair, donc de température
-80 °C, alors, la puissance rayonnée par notre mètre carré de neige
est :
. Il faudra donc une durée 1 h 30.
Si on suppose que le ciel est couvert de nuages de moyenne altitude,
des alto-stratus, leur température est typiquement de -10 °C, cela
donne une puissance rayonnée par la neige de :
. D’où une durée de regel d’environ 8 h 30.
On obtient alors une croûte de regel qui est toujours à 0 °C mais sans eau liquide. Pour consolider l’édifice il vaut mieux considérer qu’il se refroidi de surcroît un peu.
L’énergie nécessaire pour refroidir entre 0 °C et une température finale de -5 °C (donc °C) ces 100 kg de neige (glace) est donnée par : , où est la capacité calorifique massique de la glace (). Soit kJ. Au passage on constate que refroidir 100 kg de glace de 5 °C dégage à peu près autant d’énergie que de solidifier 4 kg d’eau liquide !
Par ciel clair, il faut donc 1 h 20 de plus pour atteindre cet état, soit environ 3 h au total.
Par ciel couvert de nuages de moyenne altitude, il faudra plus de 6 h 30 en plus, soit environ 15 h au total, ce qui devient bien long...
On peut ainsi sommairement conclure que lors d’une nuit claire, la neige a beaucoup plus de chance de regeler que lors d’une nuit bâchée.
Ces petits calculs sont assez grossiers, et n’ont aucune valeur de démonstration. Ils sont là à titre indicatif. Ils ne tiennent en particulier pas compte de ce qui se passe sous la couche de neige : on suppose ici qu’aucun flux thermique ne remonte. De fait, les durées calculées sont des limites minimales.
On ne tient également pas compte de l’humidité de l’air qui absorbe le rayonnement infrarouge. Les valeurs numériques sont parfois ad-hoc, comme l’épaisseur de la couche de neige considérée (20 cm) ; si on considère que 10 cm c’est aussi une bonne couche de regel, il faut diviser les durées obtenues par deux. La température de la neige de névé en fin de nuit est également ad-hoc. Faudrait que je mesure ça, un jour ou l’autre. Quoiqu’il en soit, il est probable que même si la couche de neige n’est pas nécessairement à l’équilibre thermodynamique avec l’air atmosphérique en fin de nuit, cette température dépende tout de même de la température de l’air. À vérifier...
En revanche la convection dite forcée, quand le vent se met à souffler est elle très efficace : même avec un ciel assez clair et du soleil, en cas de vent fort, la neige peut rester très dure.
La température dans la couche inférieure de l’atmosphère, la troposphère, décroit à peu près linéairement de 6,5 °C tous les kilomètre. Avec une température moyenne de 15 °C au niveau de la mer, on arrive à une température de -80 °C à 15 km, altitude limite de la troposphère.
Cette valeur est ad-hoc ; disons que c’est l’épaisseur d’une couche de regel suffisante pour « porter » les pas de l’alpiniste...
- Shaw, J. A., Nugent, P. W., Pust, N. J., Thurairajah, B., & Mizutani, K. (2005). Radiometric cloud imaging with an uncooled microbolometer thermal infrared camera. Optics Express, 13(15), 5807. 10.1364/opex.13.005807