Dans les années 1940, le biologiste suisse Max Kleiber observa que le métabolisme de la plupart des animaux était corrélé à leur masse. Le métabolisme est la dépense énergétique de base (par unité de temps, il s’agit donc d’une puissance) nécessaire à un être vivant au repos pour survivre dans ses conditions habituelles d’habitat.
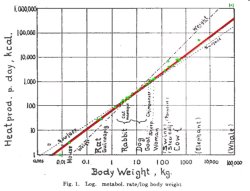
- Production de chaleur par jour (taux de métabolisme) pour un certain nombre d’animaux. Diagramme publié par Max Kleiber en 1947 ( « Body size and metabolic rate ». Physiological Reviews 27, pp. 511–541.) Tiré de wikipédia.
Kleiber a ainsi observé que la puissance $P$ requise pour la survie d’un animal était proportionnelle à sa masse $M$ à la puissance 3/4 :
$P = k\cdot M^{3/4}$, où $k$ est une constante de proportionnalité.
La constante de proportionnalité dépend du métabolisme de la « classe » d’animaux considérés. Ainsi, pour les animaux homéothermes avec une température interne voisine de 39°C (les mammifères, donc), $k = 4.1\ \text{W}\cdot \text{kg}^{-3/4}$, pour les poïkilothermes (ou animaux à sang froid !) à une température de 20°C, $k = 0.14\ \text{W}\cdot \text{kg}^{-3/4}$ et pour des êtres unicellulaires à la température de 20°C, $k = 0.018\ \text{W}\cdot \text{kg}^{-3/4}$.
On peut s’amuser à vérifier que cette loi est vérifiée pour l’homme : avec $M = 70$ kg, on obtient une puissance de 100 W. D’où une énergie dépensée chaque journée de 8,6 MJ ou encore environ 2000 kcal (car 1 cal = 4.18 J). Or les besoins énergétiques journaliers d’un homme sont effectivement de l’ordre de 2000 kcal.
Pour une souris, les besoins énergétiques sont de 5.3 kcal. La souris étant omnivore, et les aliments ayant grosso modo une valeur énergétique de 100 kcal pour 100g, la souris doit ingurgiter chaque jour 5.3 g d’aliments, soit un cinquième de sa masse.
L’homme doit manger 2 kg d’aliments par jour, soit 3 % de sa masse. L’éléphant est herbivore, et dépense 38500 kcal chaque jour. Il doit donc manger environ 38.5 kg d’aliments par jour, soit 1 % de sa masse...
Les animaux ont besoin de relativement plus d’énergie quand ils sont petits que quand ils sont gros. Ainsi la souris va devoir passer le plus clair de son temps à manger (j’aimerais vous y voir si vous deviez avaler 20 kg de nourriture par jour !), tandis que l’homme ou l’éléphant peuvent passer une bonne partie du temps à farnienter...
À partir de cette loi de Kleiber, on peut facilement en déduire une loi générale sur la longévité des mammifères.
Pour cela, montrons tout d’abord leur rythme cardiaque est proportionnel à $M^{-1/4}$. On suppose que la puissance issue du métabolisme sert à faire circuler le sang dans le corps de l’animal. Cette puissance doit donc dépendre de la masse totale de sang dans le corps, $M_{sang}$, de la vitesse de circulation du sang dans les vaisseaux, $v_{sang}$, de la fréquence de pulsation du cœur (rythme cardiaque), $f_{card}$.
La seule façon de combiner ces paramètres compte tenu de leurs dimensions physiques est $P \propto f_{card} \cdot M_{sang} \cdot v_{sang}^2$
On a :
$[P] = ML^{2}T^{-3}$
$[f_{card}] = T^{-1}$
$[M_{sang}] = M$
$[v_{sang}] = LT^{-1}$
où les crochets [] désignent la dimension physique de la grandeur, $M, L, T$ désignent respectivement la masse, la longueur, le temps.
Donc : $[P] = [f_{card}]^{a}\cdot [M_{sang}]^{b}\cdot [v_{sang}]^{c}$ soit : $ML^{2}T^{-3} = T^{-a} M^b L^c T^{-c}$ soit $ML^{2}T^{-3} = M^b L^c T^{-a-c}$ donc :
$b = 1$
$c = 2$
$-a-c = -3$ soit $a = 1$
Donc : $P \propto f_{card} \cdot M_{sang} \cdot v_{sang}^2$.
Or la vitesse du sang dans les vaisseaux sanguins est en moyenne identique d’un animal à l’autre. Donc $v_{sang} \propto 1$.
Pour la peine $f_{card} \propto M^{-1/4}= a \cdot M^{-1/4}$, car $M_{sang} \propto M$ ; $a$ est une constante de proportionnalité.
Par exemple, le débit sanguin $D$ est tel que : $D = v_{sang} \cdot S_{vaisseaux}$, où $S_{vaisseaux}$ est la section moyenne des vaisseaux sanguins. De même que : $D = V_{sang} \cdot f_{\text{coeur}}$, où $V_{sang}$ est le volume total du sang. Donc $v_{sang} \cdot S_{vaisseaux} = V_{sang} \cdot f_{\text{coeur}}$. Comme $S_{vaisseaux} \propto L^2 \propto M^{2/3}$, où $L$ est la taille de l’animal (sa longueur ou sa hauteur, par exemple), comme $V_{sang} \propto V \propto M$, $V$ étant le volume total de la bestiole, on a : $v_{sang} \propto M \cdot M^{-1/4} \cdot M^{-2/3} \propto M^{1/12}$, soit $v_{sang} \propto M^{1/12} \sim 1$ avec la précision toute relative qui incombe à cet exercice...
Donc on a bien $f_{card} \propto M^{-1/4} = a \cdot M^{-1/4}$.
On peut vérifier cette relation entre les deux mammifères que sont la souris et l’homme. La souris pèse en moyenne 25 g, et son cœur bat au rythme effréné de 600 pulsations par minute. Donc $f_{card}^{homme} = f_{card}^{souris} \left(\frac{M_{homme}}{M_{souris}}\right)^{-1/4}$ soit $f_{card}^{homme} = 600 \cdot \left(\frac{70}{0.025}\right)^{-1/4} = 82$ pulsations par minute, ce qui est tout à fait l’ordre de grandeur du rythme cardiaque de l’homme.
Au passage, on en déduit une valeur de la constante de proportionnalité : $a = 239\ \text{min}^{-1} \text{kg}^{1/4}$. Donc : $f_{cœur} = 239 \cdot M^{-1/4}$, où $f_{card}$ est un nombre de battements par minute, et $M$ la masse en kg.
Pour en venir à l’objet de cet article, la durée de vie $\tau$ d’un animal est proportionnelle à la période entre deux pulsations cardiaques moyennes, donc inversement proportionnelle à la fréquence cardiaque. Ainsi $\tau \propto M^{1/4}$.
Voici ci-dessous un tableau reportant la longévité (espérance de vie) de quelques mammifères.
Ces valeurs sont tracées sur le graphique suivant, et ajustées par une loi de puissance. Cet ajustement n’est là qu’à titre illustratif, il ne saurait tenir lieu de démonstration : pour ce faire, il faudrait beaucoup plus de données, avec leurs barres d’erreurs. Or j’ai « sélectionné » quelques animaux, en essayant d’être représentatif, en donnant une valeur que j’ai estimé « moyenne » sur leur durée de vie et leur masse, au regard des différentes sources que j’ai pu trouvé sur le net et ailleurs. Tout ça pour dire que la loi trouvée fonctionne globalement bien avec ces données-là.
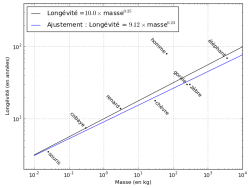
- Tracé du tableau, longévité en fonction de la masse de quelques mammifères
- Les points représentent les données du tableau. Les courbes, la loi déterminée dans cet article (loi de puissance et 1/4), et un ajustement effectué sans tenir compte de l’humain.
L’homme est un peu une exception dans cette histoire, car il vit beaucoup trop longtemps par rapport à sa masse. Il devrait vivre effectivement 30 ans si l’on en croit notre loi. De fait c’était l’espérance de vie jusqu’au XVIIIe siècle. À partir du XIXème, les progrès constants de la médecine et de l’hygiène ont permit à l’homme d’atteindre 80 ans (en France) — enfin, pour les femmes, en fait, surtout ! Et ainsi de dépasser de loin sa propre longévité.
C’est pourquoi l’ajustement des points de données par une loi de puissance fait abstraction du cas de l’homme. Le résultat est : $\tau = 9.12 M^{0.23} \sim 10 M^{0.25}$.
On peut finalement déduire de tout ça que le produit de la fréquence cardiaque par la durée de vie fournit un nombre sans dimension, le nombre $N$ de battements du cœur dans une vie entière : $N = f_{card} \times \tau \simeq 239 \times (10 \times 365,25 \times 24 \times 60) = 1.3\cdot 10^{9}$.
On constate ainsi que tous les mammifères s’éteignent après que leur cœur ait fait environ un milliard de battements : les petits animaux ont le cœur qui bat la chamade et vivent peu longtemps, car le milliard de battement est rapidement atteint ; les grands animaux ont au contraire un rythme beaucoup plus lent, et de fait mettent plus longtemps à atteindre leur milliard de battements !




