Poster un message

En réponse à :

Volume de liquide dans le fond d’une cuve cylindrique horizontale

lundi 13 août 2012 par Guillaume Blanc

Séquence poésie... Je vous laisse apprécier la rime :

Chez mes parents, trône dans un coin une vieille cuve à mazout, qui servait il y a encore quelques années à alimenter la chaudière. Elle est désormais inutile, mais il reste dans le fond une petite quantité de fuel. Si on pouvait mesurer la hauteur du liquide, il a fallu trouver une formule pour en évaluer le volume, et ce en fonction uniquement de cette hauteur $h$ de liquide résiduel, du rayon $R$ intérieur de la cuve et de sa longueur $L$ .

**Schéma global de la cuve cylindrique avec son fond de liquide en vert**

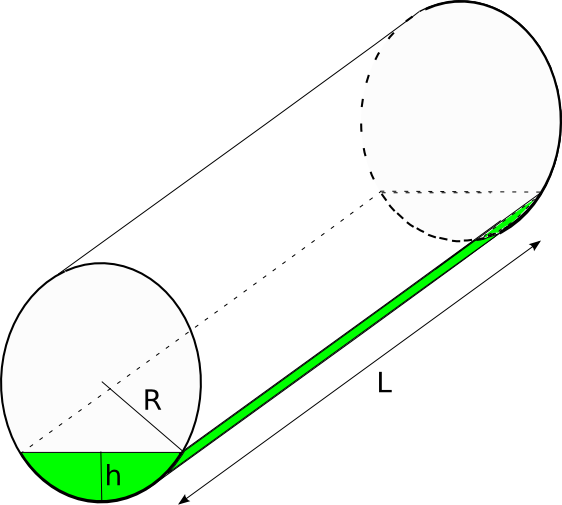
On suppose que $h < R$ .

**Coupe transversale de la cuve, le mazout résiduel est représenté en vert**

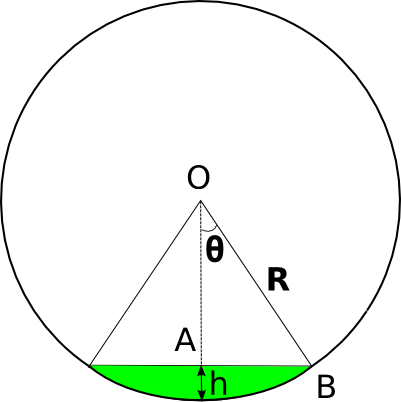
Il suffit de calculer l’aire (en vert) entre un arc de cercle et sa corde pour avoir résolu une bonne partie du problème.

**Calcul de l’aire d’une part de camembert**

L’aire d’un coin de camembert de rayon $R$ et d’angle au sommet $\theta$ est donnée par :

$A_{\mathrm{camembert}} =\int_0^{R}\theta R dR = \frac{\theta R^2}{2}$

Ce à quoi il faut retrancher la surface du triangle AOB formé par la demi-corde et le centre du cercle, $A_{\mathrm{triangle}} = 1/2 R^2 \sin \theta \cos \theta$ , pour ensuite multiplier le tout par deux, pour avoir la surface cherchée entre l’arc de cercle d’angle $2 \theta$ et sa corde :

$A_{\mathrm{arc}} = 2(A_{\mathrm{camembert}} - A_{\mathrm{triangle}}) =\theta R^{2} - R^{2} \sin \theta \cos \theta$

Exprimons maintenant $\theta$ en fonction de $R$ et $h$ . Nous avons : $R-h = R \cos \theta$ soit $\theta = \arccos \left( 1 - \frac{h}{R}\right)$ , d’où :

$A_{\mathrm{arc}}(h) = R^{2} \arccos \left( 1 - \frac{h}{R}\right) - R^{2} \sin \left( \arccos \left( 1 - \frac{h}{R}\right) \right)\left( 1 - \frac{h}{R}\right)$

Or, comme : $\sin(\arccos(x)) = \sqrt{1 - \cos^2(\arccos(x))} = \sqrt{1-x^2}$ , nous avons donc :

$A_{\mathrm{arc}}(h) = R^{2} \arccos \left( 1 - \frac{h}{R}\right) - R^{2} \left( 1 - \frac{h}{R}\right) \times \sqrt{1-\left( 1 - \frac{h}{R}\right)^2}$

$A_{\mathrm{arc}}(h) = R^{2} \arccos \left( 1 - \frac{h}{R}\right) - R^{2} \left( 1 - \frac{h}{R}\right) \times \sqrt{\frac{h}{R}\left(2 - \frac{h}{R}\right)}$

Le volume de liquide résiduel est ainsi $V = L\times A_{\mathrm{arc}}$ , soit :

$V(h) = LR^{2}\left[ \arccos \left( 1 - \frac{h}{R}\right) - \left( 1 - \frac{h}{R}\right) \times \sqrt{\frac{h}{R}\left(2 - \frac{h}{R}\right)} \right]$

Ce pour $h < R$ .

Dans le cas contraire, pour $h>R$ , on peut adapter cette formule car : $V(h) = L[\pi R^2 - A_{\mathrm{arc}}(2R-h)]$ , soit :

$V(h) = LR^{2}\left[ \pi -\arccos \left(\frac{h}{R}-1\right) + \left(\frac{h}{R}-1\right) \times \sqrt{\frac{h}{R}\left(2 - \frac{h}{R}\right)} \right]$

pour $h>R$ .

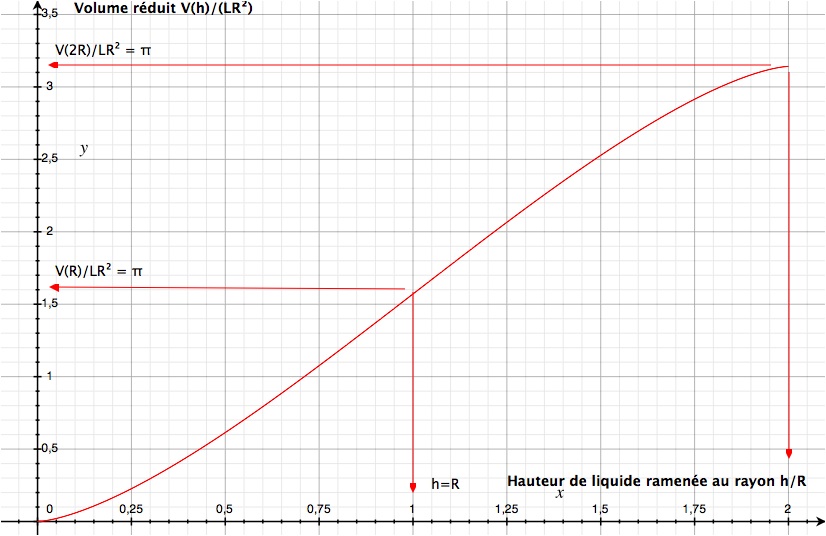
La figure suivante montre le tracé de ces deux formules :

Voilà. On s’amuse comme on peut, n’est-ce pas ? Au passage, pour faire les figures, j’ai découvert Inkscape, un fantastique logiciel libre de dessin vectoriel !

On peut aussi taper « horizontal cylinder water volume » sur WolframAlpha...

En réponse à :

Volume de liquide dans le fond d’une cuve cylindrique horizontale

12 février 202311:44, par bernard deprez

bonjour et merci pour cet article (déjà ancien). Malheureusement, j’essaie de l’utiliser (pour exactement la même finalité : une citerne) et pour vérifier, je me dis que si h = R (moitié de la cuve remplie) je devrais obtenir le volume de la moitié de la cuve ? ça ne semble pas être le cas en appliquant la formule... (dans un rapport 1/2.14917309). Je ne suis pas mathématicien... donc je suis bloqué là.

modération a priori

Ce forum est modéré a priori : votre contribution n’apparaîtra qu’après avoir été validée par les responsables.

Qui êtes-vous ?

Votre nom

Votre adresse email

Votre message

Titre (obligatoire)

Texte de votre message (obligatoire)

Pour créer des paragraphes, laissez simplement des lignes vides.

Lien hypertexte

(Si votre message se réfère à un article publié sur le Web, ou à une page fournissant plus d’informations, vous pouvez indiquer ci-après le titre de la page et son adresse.)

Titre

Lien hypertexte