Poster un message

En réponse à :

Puissance lumineuse d’une bougie

vendredi 4 avril 2014 par Guillaume Blanc

En écrivant un article sur le projet de télescope LSST (à venir), j’en suis venu à me poser la question fondamentale de savoir quelle était la puissance lumineuse rayonnée par une bougie dans le domaine visible du spectre électromagnétique. Tout ça parce que je voulais savoir à quelle distance il fallait mettre une bougie pour qu’elle soit à la limite de détection du futur télescope. Et comme google ne connaît pas la réponse, j’ai dû bricoler un peu. Pour la peine, je vous livre ici mes élucubrations (un peu calculatoires, j’admets, donc si vous êtes allergique aux équations, vous pouvez exceptionnellement ne pas lire cet article), ce qui m’évitera également, de fait, de recommencer dans 10 ans, si besoin est.

Sur internet on trouve assez facilement que l’intensité lumineuse d’une bougie est environ d’un candela (cd). En fait la bougie est même une ancienne unité de mesure de l’intensité lumineuse. Ainsi 1 bougie = 1,018 cd.

On entre ainsi de plain-pied dans le monde des unités de mesure photométrique. Mais curieusement, celles-ci n’ont rien à voir avec celles que j’ai l’habitude d’utiliser, à savoir des watts, des mètres, des secondes, des stéradians, et les combinaisons adéquates de tout ça.

En fait wikipédia qualifie de radiométriques les unités dites « objectives » qui ne dépendent pas de perception humaine, et de photométriques les unités dites « subjectives » qui dépendent de la courbe de sensibilité de l’œil humain.

Pour ma part, en astrophysique, j’ai toujours fait de la « photométrie » avec des watts et consœurs, et non de la radiométrie. D’ailleurs, les lumen, pour moi, c’est un truc vraiment bizarre.

Donc, ces candela (cd), lumen (lm) et autre lux (lx), ça sort de quel chapeau ? Et bien ce sont respectivement des unités d’intensité lumineuse, de flux lumineux et d’éclairement lumineux, pondérés par la réponse de l’œil (efficacité lumineuse spectrale), qui dépend de la vision diurne ou nocturne. C’est compliqué, n’est-ce pas ? Oui, finalement, vive l’astrophysique, c’est bien plus simple !

Mais revenons à nos moutons. Notre bougie en l’occurrence. Elle brille un candela. Or 1 lm = 1 cd/sr, un flux lumineux, c’est aussi une intensité par unité d’angle solide (en stéradians, sr). L’angle solide étant une sorte de généralisation de la notion d’angle plan dans l’espace : c’est grosso-modo la surface de quelque chose divisé par le carré de la distance à cette surface. Si on regarde l’ensemble de la sphère depuis le centre, l’angle solide est de $4\pi\ \text{sr}$ . Donc $1\ \text{cd} \sim 12\ \text{lm}\cdot\text{sr}$ .

Il me reste à obtenir le flux lumineux ou visuel dans une unité convenable (dite énergétique ou radiométrique). Pas évident au premier abord. Néanmoins, nous avons l’égalité suivante :

$\Phi_v(\lambda) = K_{555} \cdot V(\lambda) \cdot \Phi_e(\lambda)$

où $\Phi_v(\lambda)$ est le flux lumineux — visuel — en lumen par mètre, $K_{555}$ est l’efficacité lumineuse à la longueur d’onde de 555 nm (qui est le maximum d’efficacité de la vision humaine diurne, dite vision photopique [1] : $K_{555} = 683\ \text{lm}\cdot \text{W}^{-1}$ ), $V(\lambda)$ est l’efficacité lumineuse spectrale et $\Phi_e(\lambda)$ est le flux énergétique en watts par mètre.

Que je ne perde pas de vue mon objectif : je cherche le flux total de rayonnement de ma bougie (en watt, donc), dans le spectre visible (entre 400 et 700 nm).

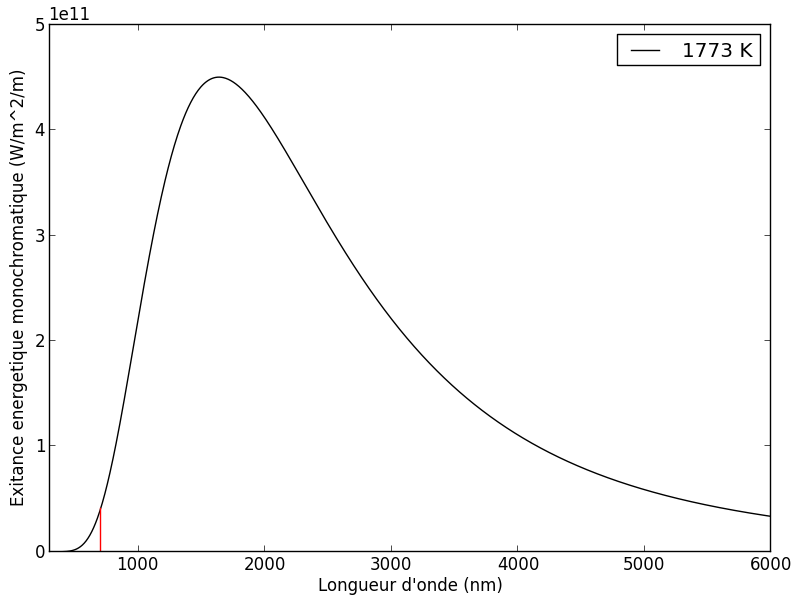
Une autre chose que l’on trouve facilement sur internet est la température de la flamme, soit 1500 °C ou 1773 K. À partir de là, en faisant l’hypothèse (raisonnable) que la zone radiative de la flamme de la bougie est à peu près un corps noir, on en déduit l’exitance énergétique monochromatique $M_{\lambda}^0(\lambda, T)$ donné par la loi de Planck, qui n’est rien d’autre que le flux de rayonnement $dL$ émis par unité de surface $S$ et par unité de longueur d’onde $\lambda$ , qui ne dépend que de la température du corps $T$ :

$M_{\lambda}^0(\lambda, T) = \frac{dL}{dSd\lambda}(\lambda ; T) = \frac{4\pi hc^2}{\lambda^5} \frac{1}{e^{\frac{hc}{\lambda k T}}-1}$ ,

pour un rayonnement dans tout l’espace, avec $h= 6,626\times 10^{-34}\ \text{J}\cdot \text{s}$ , la constante de Planck, $c = 299 792 458\ \text{m/s}$ , la vitesse de la lumière et $k= 1,380\times10^{-23}\ \text{J}/\text{K}$ , la constante de Boltzmann.

En intégrant cette fonction sur le domaine visible, entre 400 nm et 700 nm, on obtient un flux émis de $1610\ \text{W}\cdot \text{m}^{-2}$ . Reste à connaître la surface $S_e$ de la zone émissive...

J’utilise l’équation précédente liant flux « visuel » et flux « énergétique » :

$\Phi_v = K_{555} \int_0^{\infty}V(\lambda) \cdot \Phi_e(\lambda)d\lambda = K_{555} \int_0^{\infty}V(\lambda) \cdot M_{\lambda}^0(\lambda, T)\cdot S_e \cdot d\lambda$

Où :

$\Phi_v \simeq 12\ \text{lm}$
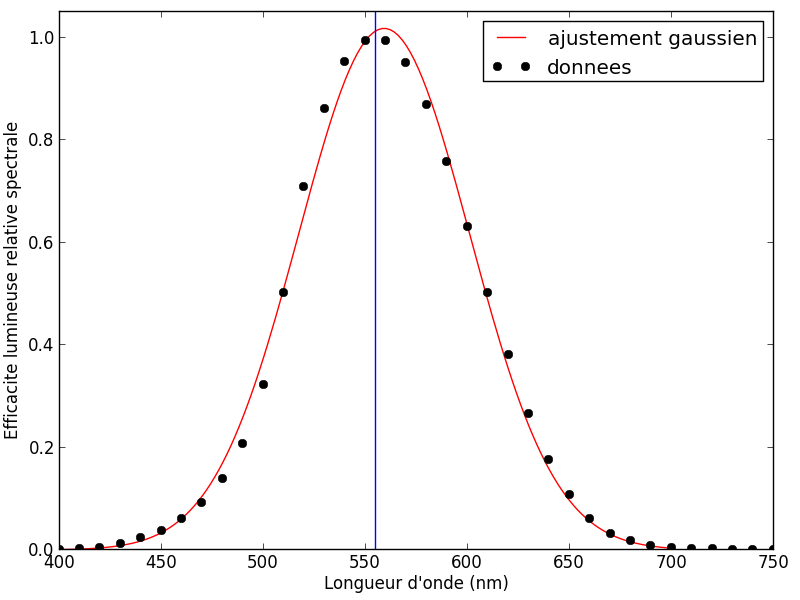
je détermine une fonction analytique pour 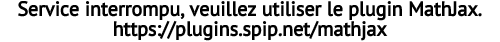$V(\lambda)$ , l’efficacité lumineuse spectrale, en ajustant une gaussienne sur les points fournis par wikipédia

Fonction d’efficacité lumineuse relative spectrale photopique

Les points proviennent de wikipédia, la courbe est un ajustement gaussien.
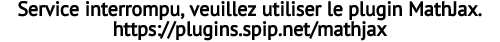$S_e$ est la surface cherchée, obtenue par approximations successives.

J’obtiens une surface émissive de $22\ \text{mm}^2$ , ce qui me semble un peu beaucoup, à vue de nez, j’aurais dit plutôt de l’ordre de grandeur du $\text{mm}^2$ ...

Avec ce résultat, on en déduit la luminosité ou puissance totale rayonnée par la bougie, ce qui donne 12 W. Sur la partie visible, entre 400 nm et 700 nm, elle rayonne 0.07 W [2], soit 0.6 % de son énergie... Le reste étant émis dans l’infra-rouge...

**Fonction de Planck : exitance énergétique monochromatique selon la longueur d’onde**

Le domaine visible est circonscrit par le trait bleu à gauche...

Donc globalement, une bougie ça chauffe plus que ça n’éclaire... Un peu comme une ampoule à incandescence.

En réponse à :

Puissance lumineuse d’une bougie

6 avril 201414:44, par Hugues THIEBAULT

Un calcul différent conduit à des résultats similaires pour la puissance dissipée par combustion. C’est un TP que je fais en 1^re STL. Le pouvoir calorifique de l’acide stéarique est 40 MJ/kg. La combustion consomme (données expérimentales) en moyenne 100 mg en 10 min, donc produit 4 kJ en 10 min, ce qui fournit une puissance thermique d’environ 7 W.

modération a priori

Ce forum est modéré a priori : votre contribution n’apparaîtra qu’après avoir été validée par les responsables.

Qui êtes-vous ?

Votre nom

Votre adresse email

Votre message

Titre (obligatoire)

Texte de votre message (obligatoire)

Pour créer des paragraphes, laissez simplement des lignes vides.

Lien hypertexte

(Si votre message se réfère à un article publié sur le Web, ou à une page fournissant plus d’informations, vous pouvez indiquer ci-après le titre de la page et son adresse.)

Titre

Lien hypertexte