Poster un message

Départ pour la Suisse et ses montagnes différé de quelques jours, j’en ai profité pour assembler les morceaux achetés samedi. Petit tour au magasin de bricolage au préalable, les précieux serre-joints ont mystérieusement disparus de ma boîte à outils...

Mais auparavant, il m’a d’abord fallu cogiter pour comprendre comment je pouvais bien faire une petite table murale, repliable le long du mur. Et solide une fois dépliée.

La semaine dernière j’ai trouvé une solution qui m’a paru élégante.

Schéma de la petite table

En tirets, le table repliée le long du mur.

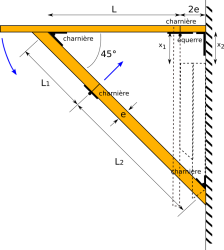
Un tasseau en diagonale, fixé sous la table et sur le mur, coupé en deux, qui se replie grâce à une poignée de charnières. J’ai tâtonné un peu pour trouver l’expression des longueurs $L_1$ et $L_2$ en fonction de la longueur $L$ entre les deux charnières sur la table, et $e$ qui est l’épaisseur du tasseau.

Comme le pied est fixé sur le mur au-delà du troisième côté du triangle rectangle, la charnière de pliage ne peut pas être au milieu du tasseau, sinon on ne pourra pas le plier à fond. Cherchons alors à déterminer à quel endroit du support diagonal mettre la charnière ; support diagonal placé à un angle de 45° par rapport au mur et au plateau de la table.

Posons $L_{tot} = L_1 + L_2$.

La condition importante est qu’une fois repliée, on doit avoir $x_1 = x_2$. Or $x_1 = L-L_1$ et $x_2 = (L_1+L_2) \cdot \sin(45^{\circ})-L_2$. Et $L_1+L_2 = L_{tot} = \frac{(L+2e)}{\cos(45^{\circ}}$. Donc $L-L_1 = \frac{(L+2e)}{\cos(45^{\circ})}\times \sin(45^{\circ}) - L_2 = L+2e - L_2$ car $\cos(45^{\circ}) = \sin(45^{\circ}) = \sqrt{2}/2$. Donc, nécessairement $L_2 = L_1 + 2e$. Soit $L_{tot} = L_1 +L_1 + 2e = 2(L_1+e)$.

Or d’après le théorème de Pythagore, on a aussi : $L_{tot} = \sqrt{2} (L+2e)$, d’où, en égalisant ces deux expressions : $2(L_1+e) = \sqrt{2} (L+2e)$. On en tire $L_1$ :

$$L_1 = \frac{\sqrt{2}}{2} L + (\sqrt{2}-1)e$$

Un petit tour au magasin de bricolage, je trouve une superbe planche en bambou, 40 cm de large, 18 mm d’épaisseur (la table fera, en tout, 90 cm de long) ; un tasseau carré en chêne de 44 mm de côté fera l’affaire.

Je fixe $L = 60$ cm. Cela me donne $L_1 = 44,25$ cm et $L_2 = 53,05$ cm. La longueur totale du tasseau, d’un biseau à l’autre est de 106,1 cm.

Je me mets au travail. Si j’avais bien pensé à creuser une rigole pour « enterrer » les charnières afin que les morceaux se replient correctement sur eux-mêmes, en revanche, je n’avais pas penser à comment fixer une charnière dans un angle de 45°... Je n’ai pas trouvé de solution élégante pour ça, c’est un peu bourrin, mon truc.

J’ai même oublié de déjeuner. Mais quatre heures plus tard, le truc tient la route. Ça marche. En plus, j’me suis même pas (trop) énervé ! À croire que les racines, ça me calme... ?