Poster un message

Dans la pratique du ski de randonnée, il est crucial de savoir mesurer l’inclinaison d’une pente sur la carte, pour préparer une course. On accordera ainsi une grande importance aux pentes dont l’inclinaison est supérieure à 30°, sur lesquelles des avalanches sont susceptibles de se déclencher [1].

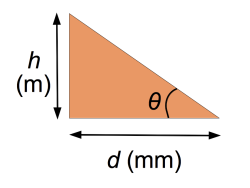
Pour effectuer un tel calcul, il suffit de mesurer la distance $d$ (en mm) entre deux courbes de niveau, et connaissant la différence d’altitude $h$ entre ces deux courbes, ainsi que l’échelle $e$ de la carte (par exemple $e = 1/25000$). La distance $D$, en mètres, sur le terrain, correspondant à $d$, est donnée par : $D = \frac{d}{e\times 10^3}$. L’angle $\theta$ de la pente est donc obtenue par la formule :

$\tan \theta = \frac{h}{D} = \frac{h\cdot e \cdot 10^3}{d}$

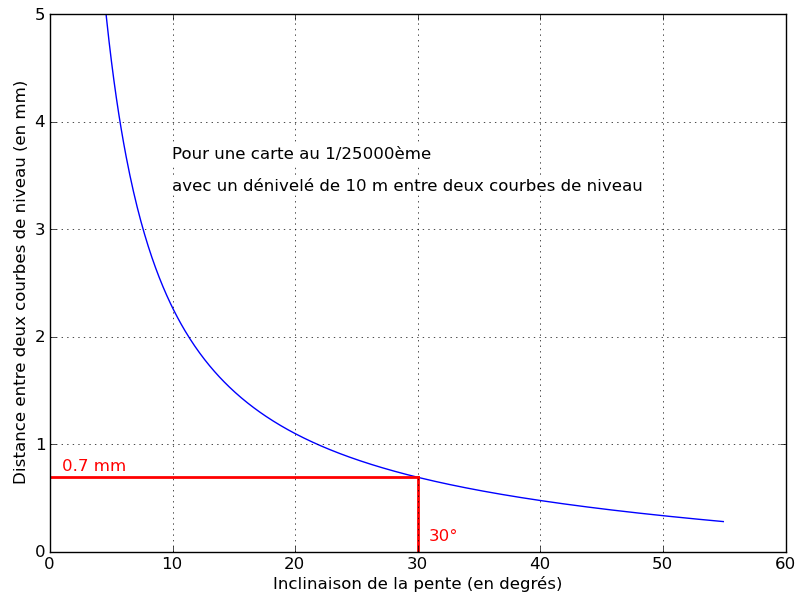
Cet angle $\theta$ de l’inclinaison de la pente est représenté sur la figure ci-dessous en fonction de la distance mesurée en mm entre deux courbes espacées de 10 m sur une carte au 1/25000ème.

Sur les cartes françaises de l’IGN au 1/25000ème, les courbes de niveau sont espacées de 10 m, ce qui représente des fractions de millimètre à mesurer pour des pentes supérieures à 22°. Pour plus de précision, on peut utiliser l’intervalle de 50 m entre deux courbes maîtresses, au tracé plus gras.

Voici quelques valeurs (en mm) à retenir pour ces cartes-là :

On pourra coller ce petit tableau en guise d’aide-mémoire sur le couvercle de la boussole...

Notez par ailleurs, que sur les cartes des pays voisins, Suisse, Italie, Espagne, etc, l’échelle et l’équidistance des courbes de niveau varie. Il suffit d’adapter le tableau en conséquence.

 Une « recette » toute simple

On peut aussi utiliser la recette suivante [2] :

- mesurer la différence d’altitude correspondant à une distance horizontale de 100 m (soit 4 mm sur une carte au 1/25000ème). Cette mesure correspond au pourcentage de la pente ;

- diviser le résultat obtenu par deux : on obtient alors l’angle d’inclinaison de la pente en degrés.

Dans ce cas, on a : $\tan \theta = \frac{x}{100}$ où $x$ est la différence d’altitude mesurée, en mètres ; c’est aussi le pourcentage de la pente.

Mathématiquement, la recette précédente se traduit par : $\theta = \frac{x}{2} = 0.5 \cdot x$.

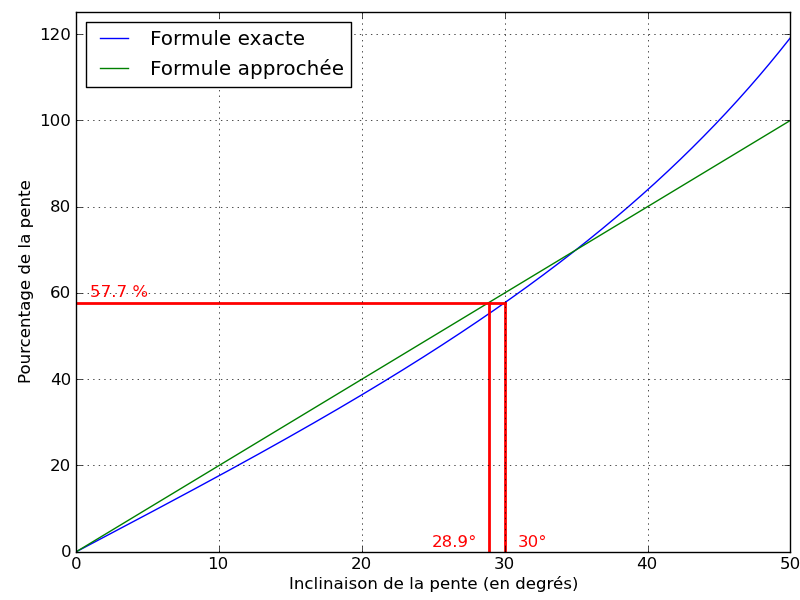
Voici la représentation graphique de ces deux formules :

On note que la « recette » s’écarte de la vraie valeur de la pente au maximum de 1.8° pour une pente de 20° (soit 36 %). L’approximation est inférieure à la valeur réelle d’au plus 2° pour des pentes d’inclinaison inférieures à 42°. Au-delà, l’approximation diverge assez rapidement (à 45°, donc pour une pente de 100 %, elle nous donne 50°), mais ce n’est pas très grave, en fait. Le principal étant d’être relativement précis autour de l’angle critique pour les avalanches, à savoir 30°.

On sous-estime ainsi légèrement (de 1.1°) l’angle de la pente autour de cet angle, mais on rentre là dans l’erreur typique de mesure d’une pente sur une carte, c’est donc tout à fait raisonnable.

Au passage, comme $\tan 35° = 0.7$, on est « exact » pour une pente de 35° !

Enfin, il faut noter que cette modeste « recette » est indépendante de l’échelle de la carte...