Une collègue « matheuse » m’avait interpellé dans les couloirs de notre belle université, un jour de l’automne dernier, tandis que j’errais entre deux cours, pour me poser cette question.
Plus concrètement, vous pouvez regarder les éphémérides (tables de prévisions des phénomènes célestes) des levers et couchers du soleil à Paris pour le mois de janvier 2010, chose que vous pouvez trouver aisément sur le site de l’Institut de Mécanique Céleste et de Calcul des Éphémérides (IMCCE), pour y constater que les jours semblent rallonger plus le soir que le matin.
En y regardant de plus près, je trouve que le soleil s’est levé (à Paris) le 1er janvier 2010 à 7 h 46, pour se coucher à 16 h 03, ces heures étant exprimées en Temps Universel (TU), qui est l’heure pour le fuseau horaire du méridien de Greenwich (à laquelle il faut donc rajouter 1 h en France en hiver, et 2 h en été pour obtenir l’heure légale de nos montres). Un mois plus tard, le 31 janvier 2010, le soleil s’est levé à Paris à 7 h 24 TU pour se coucher à 16 h 45 TU. Donc le matin, on a gagné 22 minutes de Soleil, tandis que le soir, on gagne 42 minutes !
Vous pouvez faire ce constat pour n’importe quelle période de l’année, le mois de janvier n’est ici qu’un exemple.
Tout d’abord il est effectivement normal que la durée de l’ensoleillement augmente au mois de janvier, car nous sommes après le solstice d’hiver, le jour le plus court de l’année (le soleil est au plus bas sur l’horizon), qui a lieu au mois de décembre.
Mais comment se fait-il que l’on gagne plus de soleil le soir que le matin ? La trajectoire du Soleil dans le ciel n’est-elle pas symétrique par rapport à la mi-journée, c’est-à-dire midi ?
En fait, en regardant de plus près les éphémérides de l’IMCCE, on y trouve, outre les heures de lever et coucher du soleil, l’heure à laquelle il passe au méridien du lieu. Le méridien, c’est un cercle fictif, à la surface de la Terre, qui passe par les pôles et par le lieu que l’on considère, donc Paris dans le cas présent. Quand le soleil passe au méridien, il est exactement au sud de l’observateur (dans l’hémisphère nord), et culmine dans le ciel. On appelle cet instant le « midi vrai. » Donc, pour le 1er janvier 2010, le soleil était au plus haut de sa trajectoire à 11 h 54 TU, tandis que le 31 janvier cela se passait à 12 h 04 TU. On peut ainsi calculer la durée de l’ensoleillement du matin par rapport à ce midi-là : pour le 1er janvier, on trouve 4 h 08 ; et pour l’après-midi, on trouve 4 h 09. Pour le 31 janvier, on obtient respectivement 4 h 40 pour le matin et 4h41 pour l’après-midi.
Ouf ! les longueurs des matin et après-midi retrouvent leurs symétries. Mais alors pourquoi donc le centre de symétrie, le « midi vrai » yoyote-t-il autour du midi (12 h) de nos montres (à un fuseau horaire près) ?
Tout le monde a appris à l’école que la Terre fait un tour sur elle-même en vingt-quatre heures. Et bien ce n’est pas tout à fait exact : par rapport aux étoiles (vous prenez une étoile lointaine qui passe au méridien, et vous mesurez le temps qu’elle met pour revenir au méridien), la Terre fait un tour sur elle-même en un petit peu moins de 24 h, à savoir 23 h 56 min 04 s. Je vous accorde que la différence est minime. Il s’agit cependant là du « jour sidéral, » qui est la véritable période de rotation de la Terre sur elle-même.
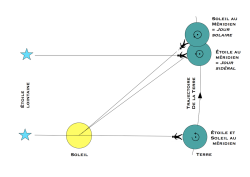
- Jour solaire et jour sidéral
- Illustration de la différence entre « jour sidéral » et « jour solaire. »
Nos vingt-quatre heures habituelles désignent en fait un « jour solaire moyen. » C’est la durée qu’il faut au soleil pour revenir au méridien d’un lieu donné et ce, en moyenne sur l’ensemble de l’année. Pourquoi quasiment quatre minutes de plus par rapport aux étoiles ? Tout simplement parce que la Terre tourne autour du soleil. Le temps d’une journée, elle s’est déplacée d’un angle d’environ un degré (360 degrés / 365,25 jours) par rapport au soleil, tandis qu’elle a parcouru plus de 2,5 millions de kilomètres ! Pour qu’un même lieu revoit le soleil au-dessus de sa tête, la Terre doit donc tourner d’un petit angle supplémentaire sur elle-même. Petit angle qui correspond à quasiment quatre minutes de temps...
La durée du jour solaire dépend donc de la vitesse de rotation de la Terre sur elle-même (sa vitesse angulaire) et de sa vitesse de révolution autour du soleil.
Et comme rien n’est simple en ce bas monde (mais n’est-ce pas là ce qui fait sa beauté ?), la vitesse de la Terre sur son orbite autour du Soleil varie [1] !
La force de gravitation, qui lie la Terre au Soleil fait que celle-ci décrit non pas un cercle mais une ellipse autour du Soleil. Kepler l’avait montré observationnellement, Newton l’a démontré mathématiquement. Du fait que sa trajectoire est elliptique, la vitesse de la Terre n’est pas constante : elle est maximale (30,287 km/s) quand elle se trouve au plus proche du Soleil, le périhélie, et minimale (29,291 km/s) quand elle se trouve au plus loin, l’aphélie. Ça aussi, Kepler l’avait observé et formulé selon sa deuxième loi.
Comme la durée du jour solaire dépend de cette vitesse orbitale, elle va donc varier de concert. Regardons comment. Le petit angle supplémentaire dont la Terre doit tourner sur elle-même pour revenir en face du Soleil dépend de la distance parcourue sur son orbite. Il est d’autant plus grand que cette distance est grande. Et cette distance est d’autant plus grande que la vitesse orbitale est élevée. Comme sa vitesse de rotation reste, elle, constante dans le temps, il lui faudra plus de temps pour parcourir cet angle plus grand que la moyenne. Le jour solaire durera ainsi plus que les vingt-quatre heures moyennes.
Inversement, si la Terre se trouve du côté de l’aphélie, sa vitesse orbitale est moins rapide que la moyenne, donc elle va devoir tourner sur elle-même d’un angle plus petit que la moyenne pour voir revenir le Soleil au méridien, la durée du jour solaire sera alors inférieure à la moyenne de vingt-quatre heures.
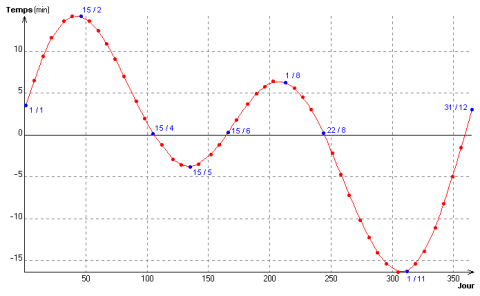
Ces écarts par rapport à la valeur moyenne de vingt-quatre heures de la durée du jour solaire sont calculables et varient au cours de l’année, avec une amplitude allant jusqu’à une quinzaine de minutes. La courbe ainsi décrite s’appelle l’équation du temps.
Cette équation du temps nous dit que le 1er janvier 2010, il faut ajouter 3,5 minutes au temps universel pour obtenir le temps solaire « vrai, » et ajouter 13,5 minutes le 31 janvier 2010 pour ce faire. On devrait donc avoir respectivement 12 h 3,5 et 12 h 13,5 pour les horaires des passages du soleil au méridien les 1er et 31 janvier respectivement, ce qui n’est pas tout à fait ce que donnent les éphémérides à Paris (11 h 54 TU et 12 h 04 TU).
La différence (9,5 minutes) provient du temps que met le soleil pour aller du méridien de Paris à celui de Greenwich. Ce dernier définit l’origine des temps, c’est donc par rapport à lui qu’ils sont déterminés. Paris se trouve à une longitude de 2°21’ à l’est de Greenwich. La Terre tournant sur elle-même d’ouest en est — c’est-à-dire dans le sens inverse des aiguilles d’une montre vue depuis le nord (le soleil se lève à l’est et se couche à l’ouest) — et un angle de un degré dans le ciel étant parcouru en une durée de 4 minutes (24 x 60 / 360), il faudra 2,3 x 4 = 9,2 minutes au soleil pour aller du méridien de Paris à celui de Greenwich. C’est donc la durée qu’il faut retrancher au temps de Greenwich pour avoir le temps de Paris : 12 h 3,5min - 9,2 min = 11 h 54,3 min et 12 h 13,5 min - 9,2 min = 12 h 4,3 min. On retrouve ainsi les horaires des passages du Soleil au méridien à Paris les 1er et 31 janvier 2010.